What is State Space Analysis?
What is State Space Analysis?
State Space Analysis Definition
State space analysis of control systems is a method to analyze both simple and complex systems using a set of variables to describe their behavior over time.
State Space Equations
Let us derive state space equations for the system which is linear and time invariant.
Let us consider multiple inputs and multiple outputs system which has r inputs and m output.
Where, r = u1, u2, u3 ……….. ur.
And m = y1, y2 ……….. ym.
Now we are taking n state variables to describe the given system hence n = x1, x2, ……….. xn.
Also we define input and output vectors as,
Transpose of input vectors,
Where, T is transpose of the matrix.
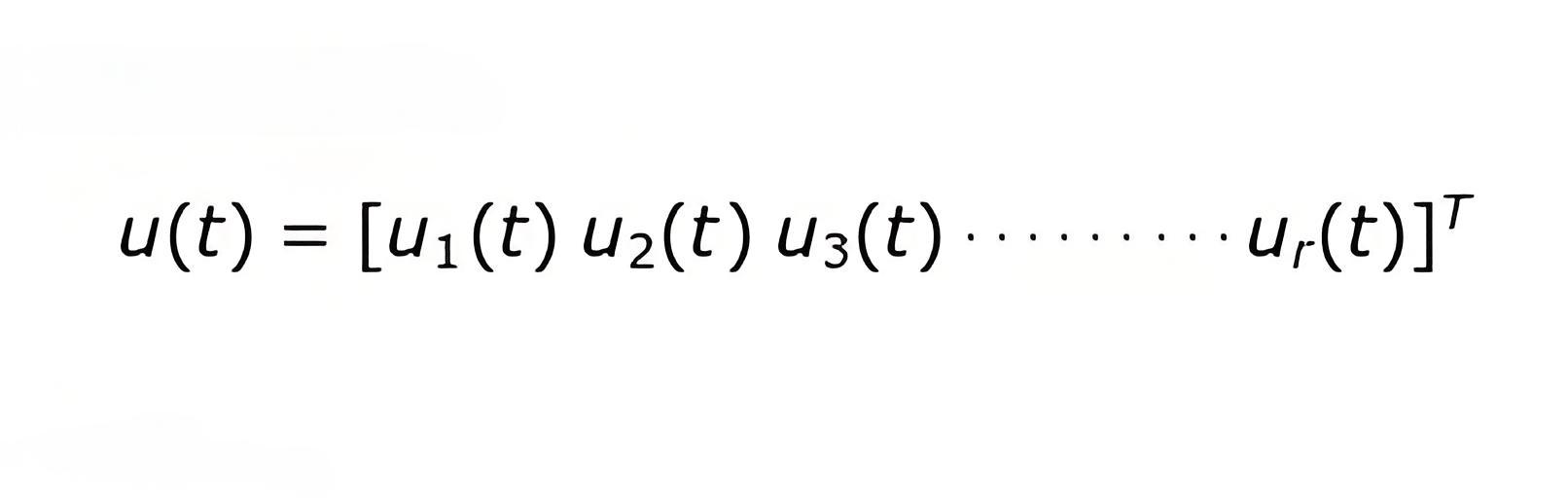
Transpose of output vectors,
Where, T is transpose of the matrix.
Transpose of state vectors,
Where, T is transpose of the matrix.
These variables are related by a set of equations which are written below and are known as state space equations
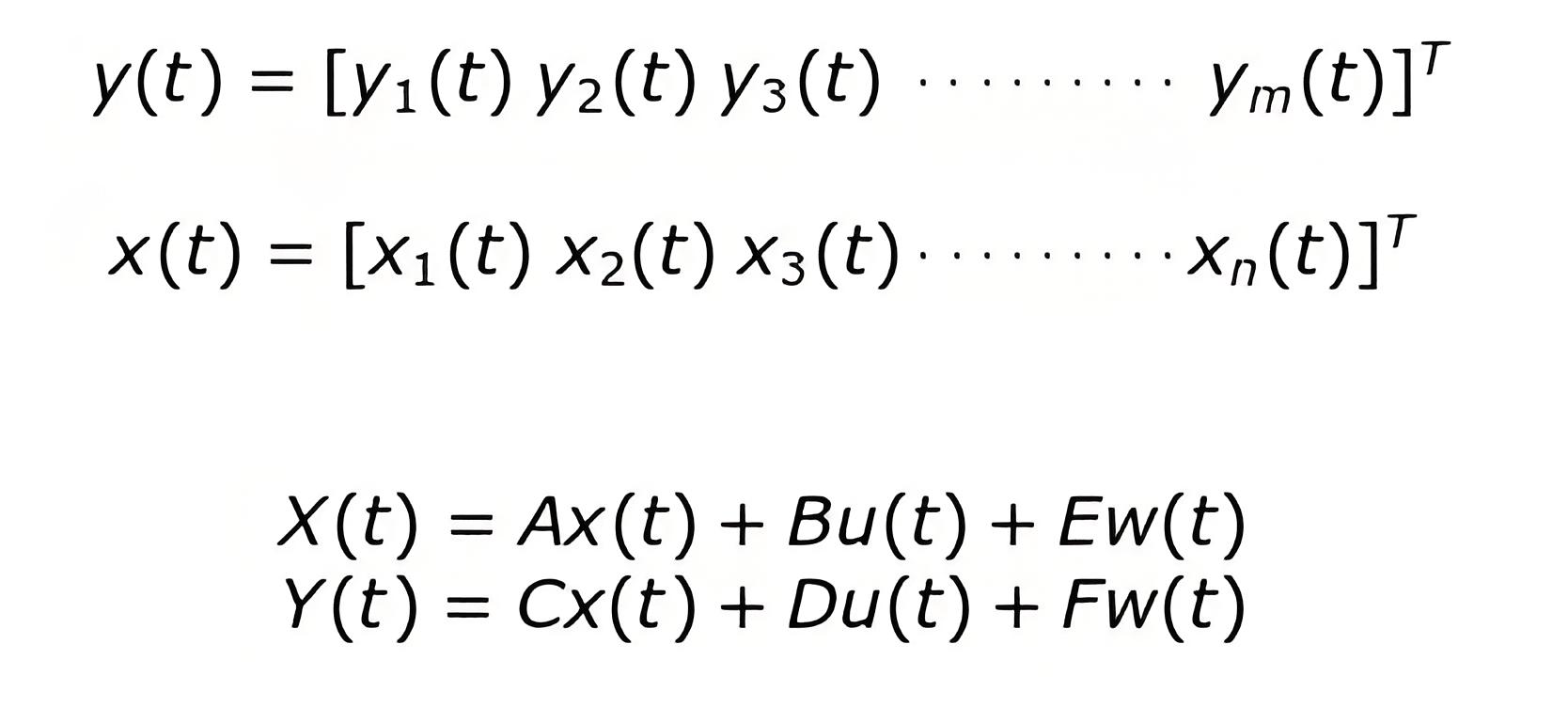
Representation of State Model using Transfer Function
Decomposition : It is defined as the process of obtaining the state model from the given transfer function. Now we can decompose the transfer function using three different ways:
Direct decomposition,
Cascade or series decomposition,
Parallel decomposition.
In all the above decomposition methods we first convert the given transfer function into the differential equations which is also called the dynamic equations. After converting into differential equations we will take inverse Laplace transform of the above equation then corresponding to the type of decomposition we can create model. We can represent any type of transfer function in state model. We have various types of model like electrical model, mechanical model etc.
Expression of Transfer Matrix in terms of A, B, C and D. We define transfer matrix as the Laplace transform of output to the Laplace transform of input.On writing the state equations again and taking the Laplace transform of both the state equation (assuming initial conditions equal to zero) we have
We can write the equation as
Where, I is an identity matrix
Now substituting the value of X(s) in the equation Y(s) and putting D = 0 (means is a null matrix) we have
Inverse of matrix can substitute by adj of matrix divided by the determinant of the matrix, now on rewriting the expression we have of
|sI-A| is also known as characteristic equation when equated to zero.
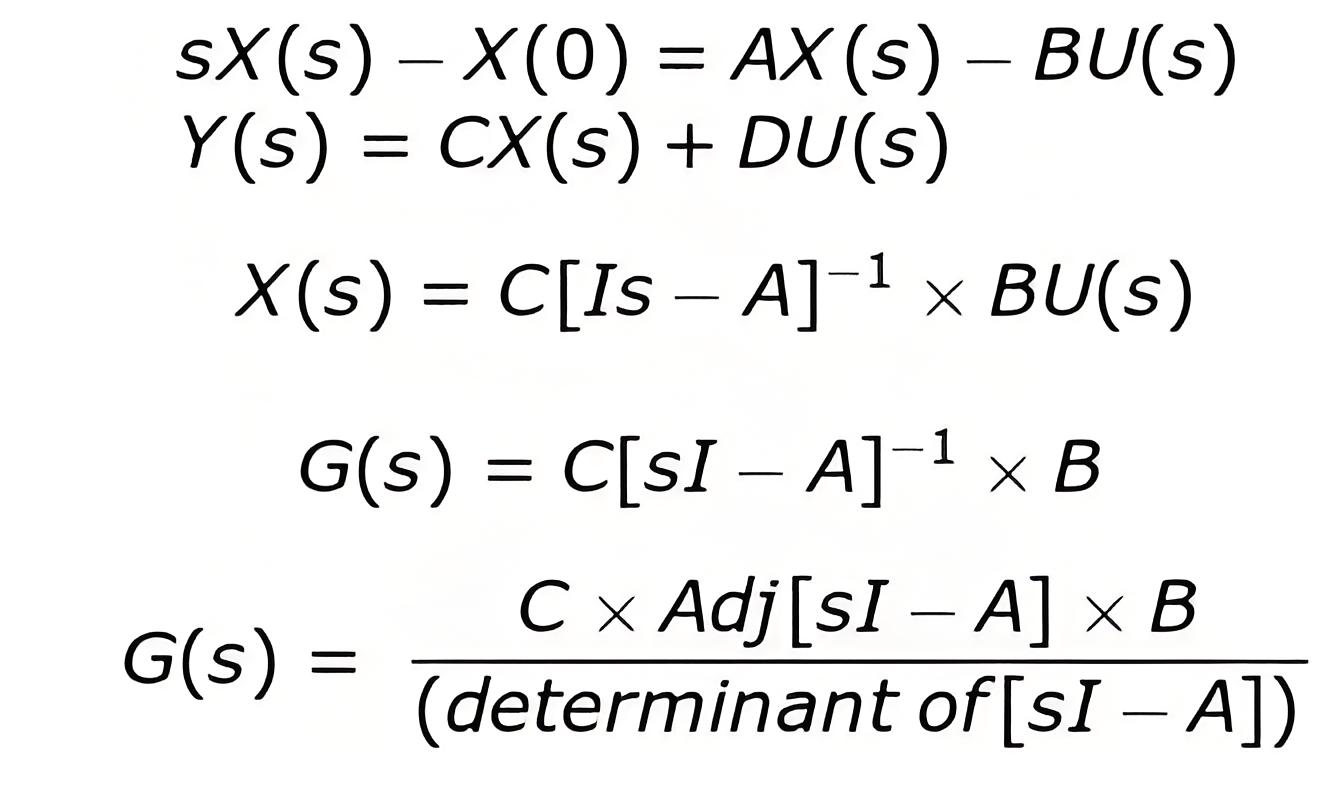
Concept of Eigen Values and Eigen Vectors
The roots of characteristic equation that we have described above are known as eigen values or eigen values of matrix A.Now there are some properties related to eigen values and these properties are written below-
Any square matrix A and its transpose At have the same eigen values.
Sum of eigen values of any matrix A is equal to the trace of the matrix A.
Product of the eigen values of any matrix A is equal to the determinant of the matrix A.
If we multiply a scalar quantity to matrix A then the eigen values are also get multiplied by the same value of scalar.
If we inverse the given matrix A then its eigen values are also get inverses.
If all the elements of the matrix are real then the eigen values corresponding to that matrix are either real or exists in complex conjugate pair.
Now there exists one eigen vector corresponding to one Eigen value, if it satisfy the following condition (ek × I – A)Pk = 0. Where, k = 1, 2, 3, ……..n.
State Transition Matrix and Zero State Response
We are here interested in deriving the expressions for the state transition matrix and zero state response. Again taking the state equations that we have derived above and taking their Laplace transformation we have,
Now on rewriting the above equation we have
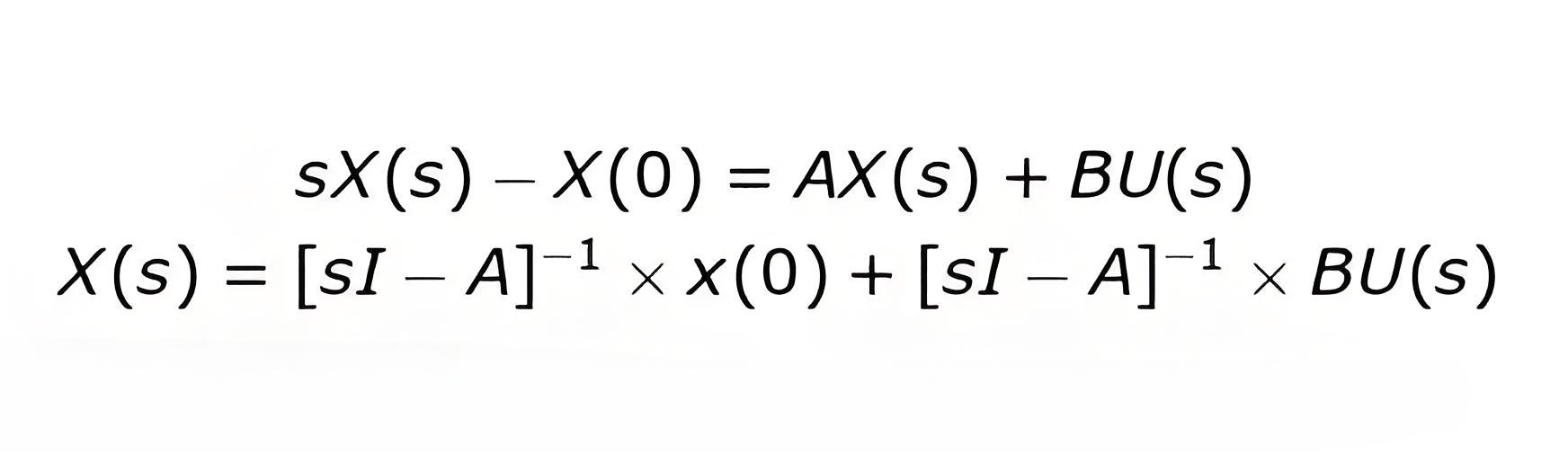
Let [sI-A] -1 = θ(s) and taking the inverse Laplace of the above equation we have
The expression θ(t) is known as state transition matrix.
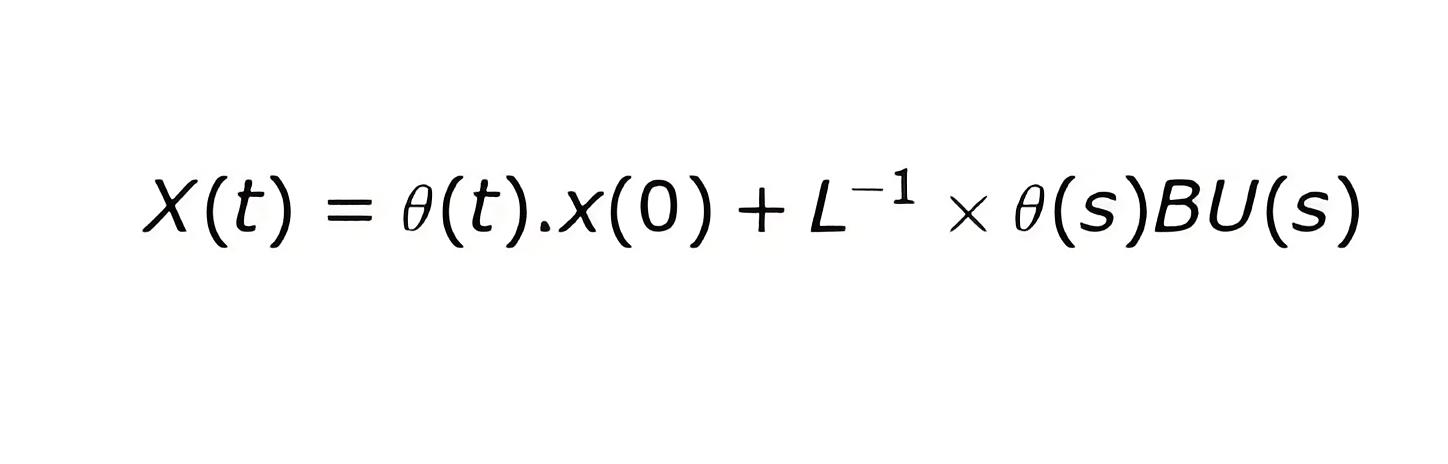
L-1.θ(t)BU(s) = zero state response.
Now let us discuss some of the properties of the state transition matrix.
If we substitute t = 0 in the above equation then we will get 1. Mathematically we can write θ(0) =1.
If we substitute t = -t in the θ(t) then we will get inverse of θ(t). Mathematically we can write θ(-t) = [θ(t)]-1.
We also another important property [θ(t)]n = θ(nt).
Welcome to our electricity community! Established to facilitate the exchange and cooperation in the electricity industry and bridge professionals, enthusiasts, and related enterprises.