On what does the capacitance of a capacitor depend?
What Does Capacitance Depend On?
The capacitance (C) of a capacitor depends on several main factors:
Plate Area (A):
The capacitance increases with the area of the plates. Larger plates can hold more charge.
Mathematically, this is expressed as C∝A.
Plate Separation (d):
The capacitance decreases as the distance between the plates increases. A smaller distance allows for a stronger electric field, enabling the storage of more charge.
Mathematically, this is expressed as C∝ 1/d .
Dielectric Constant (ε):
The dielectric constant (also known as relative permittivity or dielectric constant) of the material between the plates affects the capacitance. A higher dielectric constant results in a larger capacitance. The dielectric constant is a dimensionless number that indicates the material's ability to store electrical energy relative to a vacuum.Mathematically, this is expressed as C∝ε.
Combining these factors, the capacitance of a parallel plate capacitor can be expressed by the formula:C=εrε0A/d
where:
C is the capacitance, measured in farads (F).
εr is the relative dielectric constant of the material.
ε0 is the permittivity of free space, approximately 8.854×10−12F/m.
A is the area of the plates, measured in square meters (m²).
d is the separation between the plates, measured in meters (m).
Example
Consider a parallel plate capacitor with a plate area of 0.01m2, a plate separation of 0.001m, and a dielectric material with a relative dielectric constant of 2. The capacitance of this capacitor can be calculated as follows:
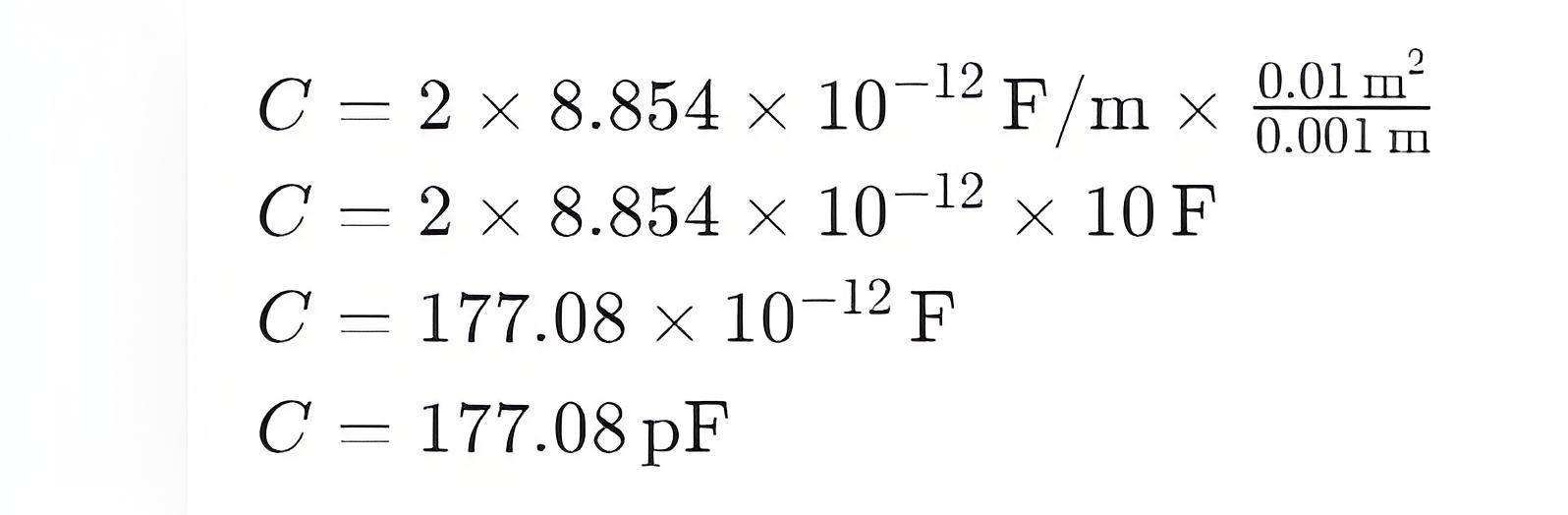
Therefore, the capacitance of this capacitor is 177.08 picofarads (pF).
The Electricity Encyclopedia is dedicated to accelerating the dissemination and application of electricity knowledge and adding impetus to the development and innovation of the electricity industry.




